PARAMOUNT SCHOOL SYSTEM
Subject: Physics – I
Unit 1: Physical Quantities and Measurement
Exercise
Q.1 Choose best possible option.
1. Which one of the following unit is not a derived unit?
A. pascal B. kilogram C. newton D. watt
2. Amount of a substance in terms of numbers is measured in:
A. gram B. kilogram C. newton D. mole
3. The number of significant figures in 0.00650 s are:
A. 2 B. 3 C. 5 D. 6
4. Which of the following numbers show 4 significant digits?
A. 9000.8 B. 4 C. 5174.00 D. 0.001248
5. Which of the following prefix represents a largest value?
A. mega B. pico C. peta D. kilo
6. Micrometer can be used to measure:
A. current B. force C. length D. mass
7. The instrument that best measures the internal diameter of a pipe is:
A. screw gauge B. vernier caliper C. metre rule D. measuring tape
8. Least count of screw gauge is 0.01 mm. If main scale reading of screw gauge is zero and the third line of its circular scale coincides with the datum line, the measurement on the screw gauge is:
A. 0 mm B. 3 mm C. 0.03 mm D. 0.3 mm
9. 9.483×10³ m is the standard form of:
A. 94.83 m B. 9.483 m C. 948.3 m D. 9483 m
10. Which of the following is a base unit?
A. pascal B. coulomb C. meter per second D. mole
11. The numbers having one significant digit is:
A. 1.1 B. 6.0 C. 7.1 D. 6×10²
12. Ratio of millimetre to micrometre is:
A. 1000 metre B. 0.001 metre C. 1000 D. 0.001
13. 0.2 mm in units of meters is:
A. 0.0002 m B. 2×10⁻⁴ m C. both A and B D. none
SHORT RESPONSE QUESTIONS
QII. Give a short response to the following questions
1. How physics plays an important role in our life?
Physics plays an important role in every aspect of life.
- Medical Technology: Devices like PET scans and microscopic robots used in cancer treatment rely on physics.
- Transportation: Physics principles are applied in designing cars, airplanes, and space shuttles.
- Communication: Technologies like smartphones, computers, and the internet function based on electromagnetic waves and circuits.
- Household Appliances: Everyday gadgets like microwaves, refrigerators, and air conditioners work using principles of thermodynamics and electricity.
2. Estimate your age in minutes and seconds.
The age of a person in minutes can be find out by expression:
If age of a student of 9th class is 15 years, then:
Age in minutes = 15 x 365 x 24 x 60 =7884000 minutes
Age in seconds = 7884000 x 60 = 473040000 seconds
3. What base quantities are involved in these derived physical quantities; force, pressure, power and charge.
| Derived Quantity | Formula | Derived Unit | Base Quantities |
| Force (F) | F=m⋅a | Newton (N) = kgm/s2 | Mass, Length, Time |
| Pressure | Pascal (Pa) = kg/ms2 | Mass, Length, Time | |
| Power | Watt (W) = kgm2/s3 | Mass, Length, Time | |
| Charge | Q=I.T | Coulomb (C) = As | Electric current, time |
4. Show that prefix micro is thousand times smaller than prefix milli.
Now compare them:
This shows that “micro” is 1000 times smaller than “milli.”
5. Justify that displacement is a vector quantity while energy is a scalar quantity.
Displacement:
Displacement is a vector quantity because it has both magnitude, which indicates how far an object has moved, and direction, which specifies the straight line path from the initial position to the final position.
Energy:
Energy is a scalar quantity because it only has magnitude and no direction. We measure energy by its amount, like 100 joules, without considering any direction, making it a scalar quantity.
6. Screw gauge can give more precise length than vernier calipers. Briefly explain why?
The least count of a vernier caliper is 0.1 mm, while the least count of a screw gauge is 0.01 mm. Since the screw gauge has a smaller least count, it can measure smaller differences in length more accurately than the vernier caliper.
7. Differentiate between mechanical stop watch and digital stop watch.
| Mechanical/Analogue Stop Watch | Digital Stop Watch |
| Has two circular dials (seconds and minutes) | Displays time digitally on an electronic screen |
| Started/stopped by pressing a knob at the top | Controlled by two buttons (start/stop and reset) |
| Least count is 1 second | Least count is 0.1 second |
| Less precise because least count is 1 second. | More precise because least count is 0.1 second. |
8. How measuring cylinder is used to measure volume of an irregular shaped stone?
Measuring cylinder can be used for measuring the volume of an irregular solid body such as metallic bob as shown in figure. When the object is completely immersed the volume of the water is read again. The volume of the object is found by subtracting the first reading from the second.
9. What precaution should be kept in mind while taking measurement using measuring cylinder?
When taking measurements using a measuring cylinder, the following precautions should be kept in mind:
- Always read the scale at eye level to avoid parallax error, ensuring an accurate measurement of the liquid’s height.
- Place the measuring cylinder on a flat, stable surface to prevent it from tipping over during measurement.
- Use a measuring cylinder appropriate for the volume being measured to ensure accuracy.
10. Why do we need to consider significant digits in measurements?
Considering significant digits in measurements is important for several reasons:
- Significant digits indicate which digits are reliable, helping convey the measurement’s accuracy.
- Correctly maintaining significant digits minimizes rounding errors in calculations, leading to more accurate results.
- Significant digits reduce confusion about its precision.
11. How random error can be reduced?
Random Errors can be reduced by:
- Taking repeated measurements.
- Finding the mean of multiple readings.
- Using statistical analysis to account for variability.
- Improving measuring techniques and equipment.
12. Differentiate between precision and accuracy.
| Precision | Accuracy |
| Consistency and repeatability of measurements. | Closeness to the true or accepted value. |
| Results are similar every time, even if not accurate. | Close to the true value, even if not consistent. |
| Example: A scale giving the same weight within 0.1 kg but overestimating by 0.5 kg. | Example: A thermometer consistently reading 2°C higher than the actual temperature. |
| Focuses on agreement between repeated measurements. | Focuses on how close the value is to the true value. |
| Achieved when results are reproducible. | Achieved when results are free from systematic errors. |
LONG RESPONSE QUESTIONS
QIII. Give a detailed response to questions below.
1. Define Physics. Describe its revolutionary role in technology.
Definition of Physics:
Physics is the branch of science that deals with the study of matter, energy, and their interactions. It helps us understand the fundamental principles governing nature and the universe.
Revolutionary Role in Technology:
Physics has played a key role in the development of revolutionary technologies. Devices like computers, smartphones, and MP3 players are based on principles of physics. Advanced technologies like rockets, space shuttles, and microscopic robots that can fight cancer cells also rely heavily on physics. From airplanes to PET scans and nuclear weapons, physics is the foundation behind many innovations that shape our world today.
2. List with brief description of different branches of physics.
Branches of Physics:
Mechanics:
The study of motion, forces, and energy, which includes understanding how objects move and interact.
Optics:
Focuses on the behavior and properties of light and its interaction with matter.
Oscillations and Waves:
Deals with repetitive motions and the propagation of waves, including sound and light waves.
Thermodynamics:
The study of heat, energy, and temperature and how they relate to each other.
Electromagnetism:
Explores the relationship between electricity and magnetism and how they produce electromagnetic fields.
Astrophysics:
The study of the physical properties of celestial bodies and the universe as a whole.
Quantum Physics:
Focuses on the behavior of matter and energy on the atomic and subatomic levels.
Atomic and Nuclear Physics:
Deals with the structure of atoms and the reactions of atomic nuclei.
Relativity:
Explores the nature of space and time, especially in contexts involving high velocities or strong gravitational fields.
3. What are physical quantities? Distinguish between base physical quantities and derived physical quantities. Give at least three examples to show that derived physical quantities are derived from base physical quantities.
Physical Quantities:
All measureable quantities are called physical quantities such as length, mass, time and temperature. Physical quantities are divided into base and derived quantities.
A physical quantity possesses at least characteristics in common. One is its numerical value and the other is the unit in which it is measured. For example, if the length of the student is 104 cm then 104 is its numerical magnitude and centimeter is the unit of measurement.
Difference between Base and Derived Quantities:
| Base Quantities | Derived Quantities |
|
The base quantities are those physical
quantities in terms of which other physical quantities are defined. |
The quantities that are derived from the base quantities are called derived quantities. |
| Not derived from other quantities. | Derived from combinations of base quantities. |
| Examples: Mass, length, time | Examples: Velocity, acceleration, force |
Examples:
| Derived Physical Quantity | Formula | Base Physical Quantities Involved |
| Area | Area = length × width | Length (m) |
| Velocity | Velocity = distance / time | Distance (m), Time (s) |
| Force | Force = mass × acceleration | Mass (kg), Length(m), Time (s) |
4. What do you mean by unit of a physical quantities? Define base units and derived units.
Unit of a Physical Quantities:
Unit is standard with which physical quantities are compared. For example, if the length of the student is 104 cm then 104 is its numerical magnitude and centimeter is the unit of measurement.
Base Units:
The units that describe base quantities are called as base units. Base units are seven in numbers. The base units corresponding to base quantities are given in the table.
| Quantity | Unit | ||
| Name | symbol | Name | symbol |
| Length | l | Meter | m |
| Mass | m | Kilogram | kg |
| Time | t | Seconds | s |
| Electric Current | I | Ampère | A |
| Intensity of light | L | Candela | cd |
| Temperature | T | Kelvin | K |
| Amount of Substance | n | Mole | mol |
Derived Units:
The units used to measure derived quantities are called derived units. Derived units are numerous. The derived units corresponding to derived quantities are given in the table:
| Quantity | Unit | ||
| Name | symbol | Name | symbol |
| Speed | V | Meter per second | ms-1 |
| Volume | V | Cubic meter | m3 |
| Acceleration | A | Meter per second per second | ms-2 |
| Force | F | Newton | N or ( Kg ms-2) |
| Pressure | P | Pascal | Pa or ( Nm-2) |
| Density | Ρ | Kilogram per cubic meter | Kgm-3 |
| Charge | Q | Coulomb | C or ( As) |
5. What are prefixes? What is their use in measurements?
Prefixes:
Prefixes are symbols used to represent powers of ten in measurements, providing a proper name for these values. Examples of prefixes are:
| Prefix | Symbol | Multiplier |
| exa | E | 1018 |
| peta | P | 1015 |
| tera | T | 1012 |
| giga | G | 109 |
| mega | M | 106 |
| kilo | k | 103 |
| hecto | h | 102 |
| deca | da | 101 |
| deci | d | 10-1 |
| centi | c | 10-2 |
| milli | m | 10-3 |
| micro |
 |
10-6 |
| nano | n | 10-9 |
| pico | p | 10-12 |
| femto | f | 10-15 |
| atto | a | 10-18 |
Uses of Prefixes in Measurement:
Prefixes are used in measurements to simplify the expression of very large or very small numbers by replacing powers of ten with a more manageable form. They are commonly used in the following ways:
- Simplifying Large Numbers:
Large numbers can be expressed using prefixes for convenience. For example:
- The number of seconds in a day, 86,400 s is written as 86.4 (kilo seconds).
- The distance to the nearest star, Alpha Centauri, 4.132×1016 m can be expressed as 41.32 Pm (Peta metres).
- Simplifying Small Numbers:
Small quantities are expressed with prefixes to avoid using many decimal places. For example:
- The diameter of a proton, 1.7×10−15 m is written as 1.7 fm (femto metres).
- Better Representation of Measurements:
Prefixes allow us to express measurements in units that better represent the size of the object being measured. For example:
- The thickness of a page is more conveniently written as 40 mm (millimetres) rather than 0.04 m
- The mass of a grain of salt is 100 mg (milligrams), instead of 0.1 g.
6. What is scientific notation or standard form of noting down a measurement? Give at least five examples.
In scientific notation, a number is expressed as some power of ten multiplied by a number between 1 and 10. It represents a number as the product of a number greater than or equal to 1 and less than 10 (called the mantissa) and a power of 10 (termed as the exponent). The general format is:
number = mantissa × 10^exponent
Example:
- The scientific notation of the measurement 384000000 m is 3.84 x 108m.
- The scientific notation of the measurement 0.00045 is 4.5 x 10-4s.
- The mass of the Earth: 5,980,000,000,000,000,000,000,000 kg = 5.98×1024 kg
- The diameter of a hydrogen nucleus: 0.0000000000000017 m=1.7×10−15 m
- The mass of a grain of salt: 0.0000001 kg = 1.0×10−7 kg
- The number of seconds in a day: 86,400 s=8.64×104s
7. Describe construction and working of vernier calipers in detail.
Vernier calipers are precise measuring devices used to measure small lengths, diameters, or depths of objects. The construction of vernier calipers includes the following main parts:
- Main Scale:
This scale has markings, usually with 1 mm divisions, and contains the fixed jaw on the left end.
- Vernier Scale:
This is a sliding scale that moves over the main scale. It has markings of some multiple of the smallest division on the main scale. For example, if the smallest main scale division is 1 mm and the vernier scale has 10 divisions, each division on the vernier scale corresponds to 0.1 mm.
- Outside Jaws:
These are used to measure the external dimensions (diameter or width) of objects.
- Inside Jaws:
These are used to measure the internal diameter of hollow cylinders.
- Depth Probe:
A rod used to measure the depth of holes or cavities.
- Retainer:
This holds the jaws in place after a measurement is taken.
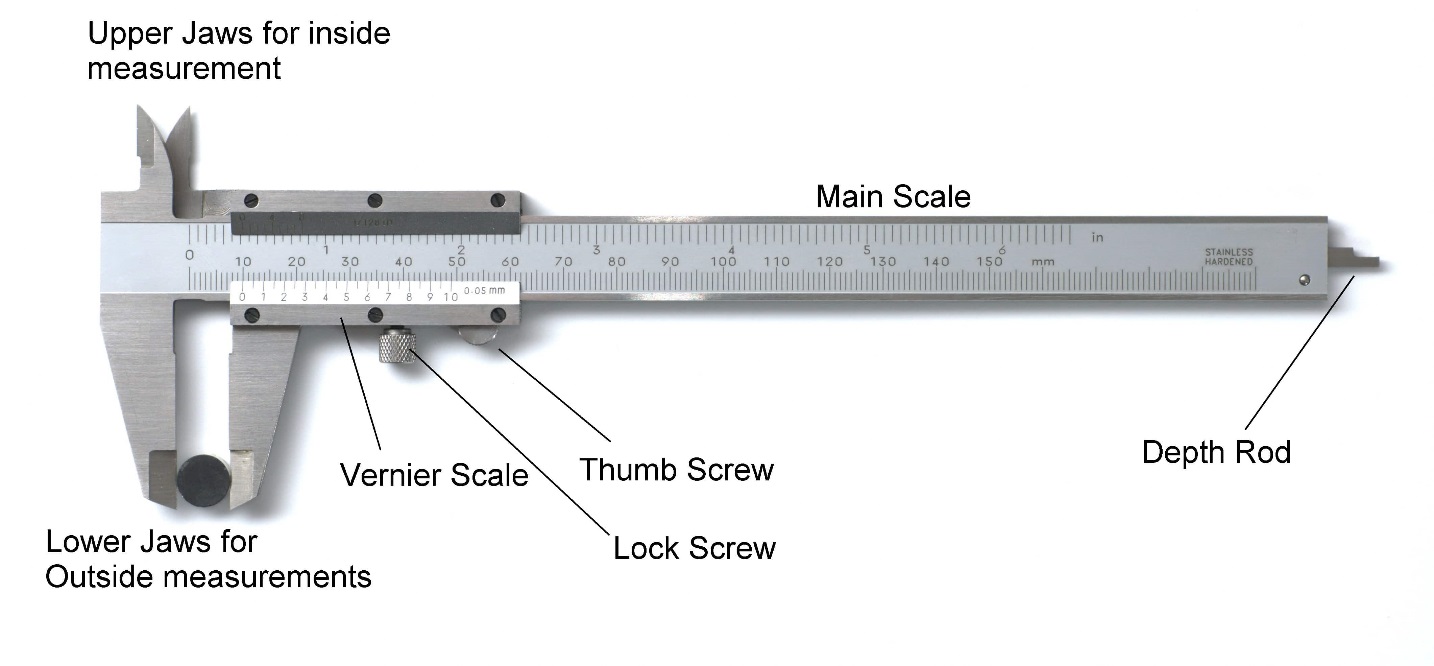
Least Count:
The least count (or vernier constant) is the minimum length that can be measured accurately by the vernier caliper. It is calculated by dividing the smallest division on the main scale by the number of divisions on the vernier scale.
If the smallest main scale division is 1 mm and there are 10 divisions on the vernier scale, the least count will be:
8. What is screw gauge? What is its pitch and least count? How is it used to measure thickness of thin copper wire?
Screw Gauge:
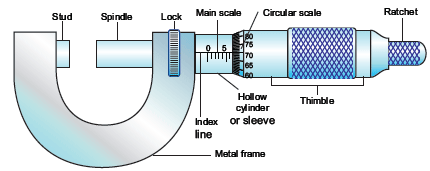
A screw gauge, also known as a micrometer screw gauge, is a precision instrument used for measuring small dimensions, such as the diameter of wires, with high accuracy. It works based on the rotation of a screw and measures smaller lengths than a vernier caliper.
Pitch:
The pitch of the screw gauge is the distance moved by the spindle for one complete rotation of the thimble. It is typically 0.5 mm or 1 mm.
Least Count:
The least count of the screw gauge is obtained by dividing the pitch by the number of divisions on the circular scale. If the pitch is 0.5 mm and the circular scale has 50 divisions, then least count is:
Measuring Thickness of Thin Copper Wire:
Set Zero: Turn the thimble until the anvil and spindle meet. Check for zero error by ensuring the zero on the circular scale aligns with the datum line on the linear scale.
Place the Wire: Place the copper wire between the anvil and spindle, and gently turn the ratchet until the spindle makes firm contact with the wire. The ratchet prevents over-tightening.
Take Main Scale Reading: Read the main scale where the circular scale edge meets it.
Take Circular Scale Reading: Find the circular scale division that coincides with the datum line and multiply it by the least count.
Calculate Total Reading: Add the main scale and circular scale readings to obtain the total thickness of the wire.
9. Define error. Differentiate between random and systematic error. How can these errors be reduced?
Error:
An error is the difference between the measured value and the true or accepted value. Errors can occur due to imperfections in the measurement process, equipment, or external factors.
Difference Between Random and Systematic error:
| Random Errors | Systematic Errors |
| Unpredictable and uncontrollable errors that occur irregularly. | Consistent errors that occur in the same direction every time. |
| Caused by fluctuations in experimental conditions or imperfections in instruments. | Caused by faulty equipment or biased measuring techniques. |
| Can be minimized by taking repeated measurements and using statistical analysis. | Can be minimized by proper calibration of instruments and correcting biases. |
| Results in different measurements each time the experiment is repeated. | Results in a constant deviation from the true value in all measurements. |
| Example: Variability in reaction time while using a stopwatch. | Example: A scale that consistently reads 0.5 kg higher than the actual weight. |
Random Errors can be reduced by:
- Taking repeated measurements.
- Finding the mean of multiple readings.
- Using statistical analysis to account for variability.
- Improving measuring techniques and equipment.
Systematic Errors can be reduced by:
- Properly calibrating instruments before use.
- Correcting any biases in measuring instruments.
- Ensuring accurate experimental setup and procedures.
- Identifying and compensating for known sources of bias.
10. Differentiate between scalars and vectors. Justify that distance, speed, mass and energy are scalars while displacement, velocity, acceleration and force are vectors.
Differentiate Between Scalars and Vectors:
| Scalars | Vectors |
| Scalars are physical quantities that are described only by magnitude (size) with proper units. | Vectors are physical quantities that require both magnitude (size) and direction to be fully described. |
| They do not require any direction to describe them. | They require a direction to specify them completely. |
| Scalars follow the normal rules of algebra for addition, subtraction, and multiplication. | Vectors require vector algebra for operations such as addition, subtraction, and multiplication. |
| Examples: Distance, speed, mass, energy, time, temperature. | Examples: Displacement, velocity, acceleration, force, momentum. |
Justification of Scalars:
Distance: Distance is a scalar quantity because it is described only by its magnitude, which represents the total path covered by an object, without considering the direction.
Speed: Speed is a scalar quantity because it refers to how fast an object is moving, defined only by its magnitude and not by the direction in which the object is traveling.
Mass: Mass is a scalar quantity because it only describes the amount of matter in an object, and this quantity does not involve direction.
Energy: Energy is a scalar quantity because it is measured solely by its magnitude, such as 100 joules, without any reference to the direction in which it is applied.
Justification of Vectors:
Displacement: Displacement is a vector quantity because it requires both magnitude, which indicates how far an object has moved, and direction, which specifies the straight-line path from the initial position to the final position.
Velocity: Velocity is a vector quantity because it describes the rate at which an object moves along with the direction of that movement.
Acceleration: Acceleration is a vector quantity because it represents the rate of change of velocity, and both the magnitude of this change and the direction in which it occurs are needed.
Force: Force is a vector quantity because it requires both magnitude (the strength of the force) and direction (the way the force is applied) to fully describe its effect on an object.
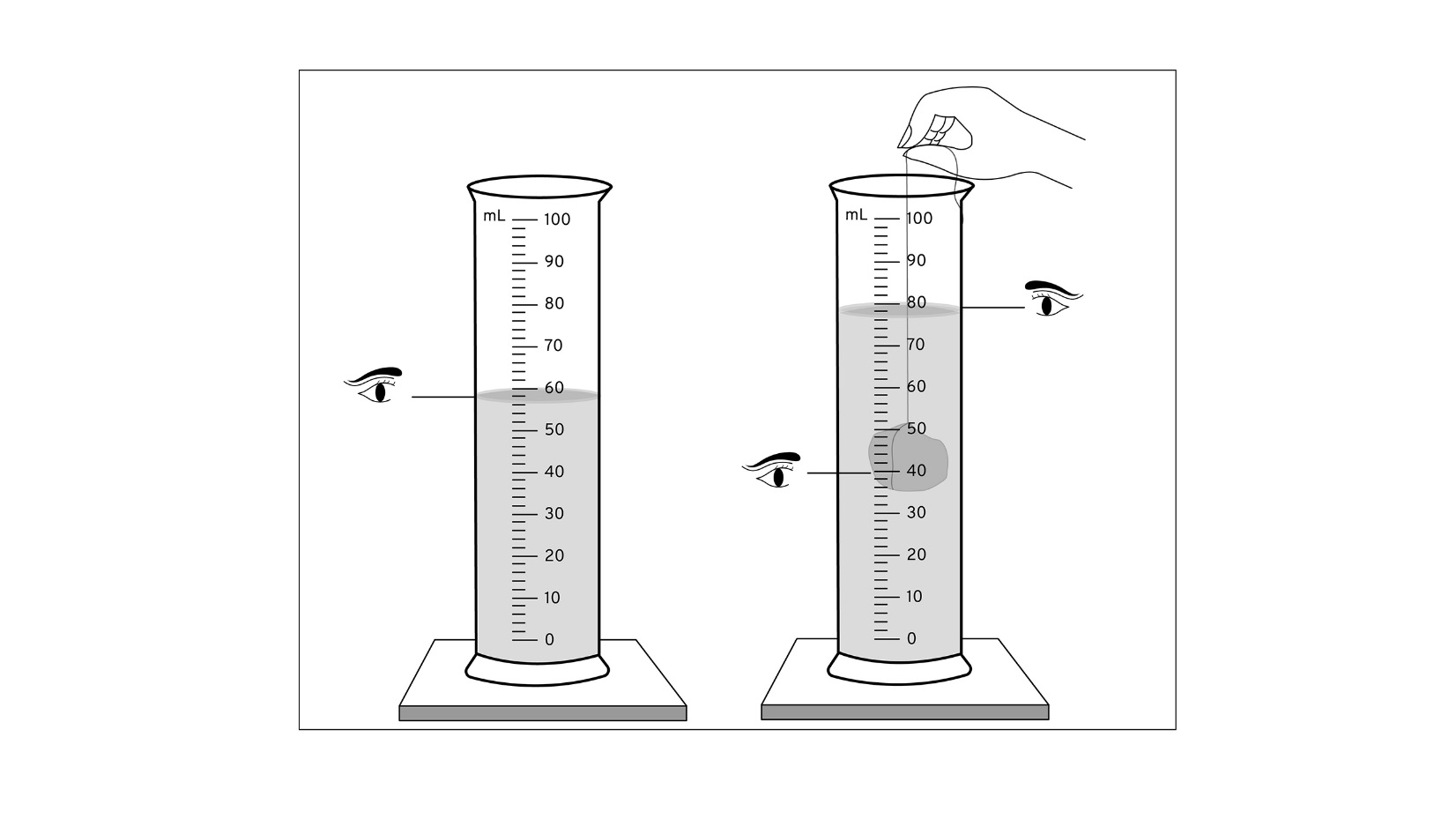11. Justify and illustrate the use of a measuring cylinder to measure the volume of a liquid.
A measuring cylinder is a tool used in laboratories to measure the volume of liquids, chemicals, or solutions. It is also known as a graduated cylinder. Measuring cylinders are typically made of transparent plastic or glass and have a vertical scale in milliliters (ml) or cubic centimeters (cm³). The volume of a liquid can be determined by measuring the height of the liquid in the cylinder. The least count of a measuring cylinder is usually 1 cm³, meaning that any volume change smaller than this cannot be measured. Measuring cylinders come in various sizes, ranging from small capacities of a few milliliters to larger capacities of several liters. The choice of cylinder size depends on the volume of the liquid being measured.
12. Differentiate between precision and accuracy.
| Precision | Accuracy |
| Consistency and repeatability of measurements. | Closeness to the true or accepted value. |
| Results are similar every time, even if not accurate. | Close to the true value, even if not consistent. |
| Example: A scale giving the same weight within 0.1 kg but overestimating by 0.5 kg. | Example: A thermometer consistently reading 2°C higher than the actual temperature. |
| Focuses on agreement between repeated measurements. | Focuses on how close the value is to the true value. |
| Achieved when results are reproducible. | Achieved when results are free from systematic errors. |