PARAMOUNT SCHOOL SYSTEM
Subject: Physics – I
Unit 2: Kinematics
Exercise
Q.1 Choose best possible option.
- Change in position of a body from initial to final point is called:
A. Distance B. Displacement C. Speed D. Velocity
- Motion of a screw of rotating fan is:
A. Circular motion B. Vibratory motion C. Random motion D. Rotatory motion
- A cyclist is travelling in a westward direction and produces a deceleration of 8 m/s² to stop. The direction of its acceleration is towards:
A. North B. East C. South D. West
- A girl walks 3 km towards west and 4 km towards south. What is the magnitude of her total distance and displacement respectively?
A. 7 km, 7 km B. 1 km, 7 km C. 7 km, 1 km D. 7 km, 5 km
- A rider is training a horse. Horse moves 60 metres towards right in 3 seconds. Then it turns back and travels 30 metres in 2 seconds. Find its average velocity:
A. 6 m/s B. 10 m/s C. 35 m/s D. zero
- If a cyclist has acceleration of 2 m/s² for 5 seconds, the change in velocity of the cyclist is:
A. 2 m/s B. 10 m/s C. 20 m/s D. 15 m/s
- A car is moving with velocity of 10 m/s. If it has acceleration of 2 m/s² for 10 seconds. What is the final velocity of the car?
A. 4.30 m/s B. 20 m/s C. 10 m/s D. 15 m/s
- When the slope of a body’s displacement-time graph increases, the body is moving with:
A. increasing velocity B. decreasing velocity
C. Constant velocity D. All of these
- A ball is thrown straight up, what is the magnitude of acceleration at the top of its path?
A. zero B. 9.8 m/s² C. 4.9 m/s² D. 19.6 m/s²
- Slope of distance-time graph is:
A. velocity B. acceleration C. speed D. displacement
- Area under speed-time graph is equal to:
A. distance B. change in velocity C. uniform velocity D. acceleration
- In 5 seconds a car accelerates so that its velocity increases by 20 m/s. The acceleration is:
A. 0.25 m/s² B. 4 m/s² C. 25 m/s² D. 100 m/s²
- Ball dropped freely from a tower reaches the ground in 4 seconds. The speed of impact of the ball is:
A. 0 m/s B. 2.45 m/s C. 19.6 m/s D. 39.2 m/s
- Which of the following distance-time graphs represents increasing speed of a car?
A.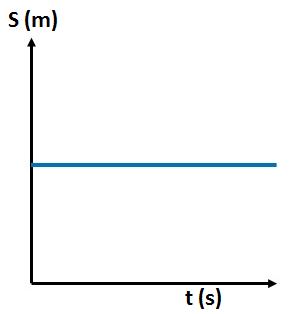 |
B.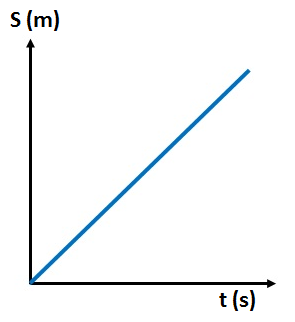 |
C. 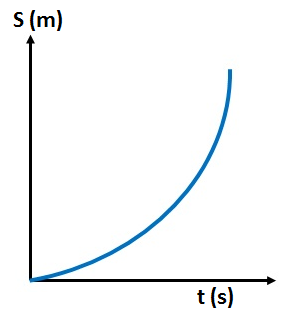 |
D.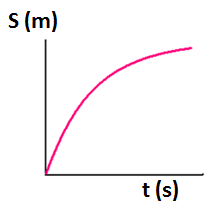 |
Correct answer is: C
Q.II Give a short response to the following questions.
- In a park, children are enjoying a ride on Ferris wheel as shown. What kind of motion the big wheel has and what kind of motion the riders have?
The big wheel of the Ferris wheel undergoes rotatory motion as it rotates around its fixed axis. The riders, on the other hand, experience circular motion because they move in a circular path while sitting on the Ferris wheel.
- A boy moves for some time, give two situations in which his displacement is zero but covered distance is not zero?
Two situations where displacement is zero but distance is not zero:
- The boy walks in a circular path and returns to his starting point. The total distance covered is the path length, but his displacement is zero because his final position is the same as his starting point.
- The boy moves forward and then retraces his steps back to the starting point. The distance traveled is the total length of the path, but displacement is zero as his initial and final positions are identical.
- A stone tied to a string is whirling in a circle, what is the direction of its velocity at any instant?
The direction of the stone’s velocity at any instant is along the tangent to the circle at that point. This means the velocity is perpendicular to the string and points in the direction of motion, constantly changing as the stone moves around the circle.
- Is it possible to accelerate an object without speeding it up or slowing it down?
Yes, it is possible to accelerate an object without changing its speed by changing its direction. For example, in uniform circular motion, an object moves at a constant speed, but its direction is constantly changing, so it experiences acceleration.
- Can a car moving towards the right have a direction of acceleration towards the left?
Yes, a car moving towards the right can have acceleration towards the left if it is decelerating or slowing down. The acceleration is in the opposite direction to the motion, causing the car to reduce its speed.
- With the help of daily life examples, describe the situations in which:
a. Acceleration is in the direction of motion:
Example: A car speeding up while moving forward.
b. Acceleration is against the direction of motion:
Example: A car braking to slow down while moving forward.
c. Acceleration is zero, and the body is in motion:
Example: A car moving at a constant speed on a straight road.
- Examine distance-time graph of a motorcyclist (as shown), what does this graph tell us about the speed of motorcyclist? Also plot its velocity-time graph.
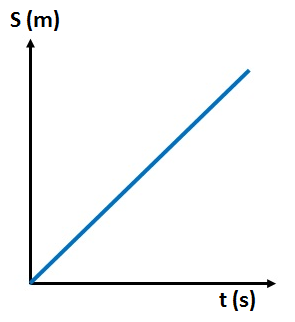
The distance-time graph shows a straight line with a constant slope, indicating that the motorcyclist is traveling at a constant speed. The distance covered is increasing linearly with time, which means the speed is uniform and there is no acceleration or deceleration.
Velocity Time Graph:
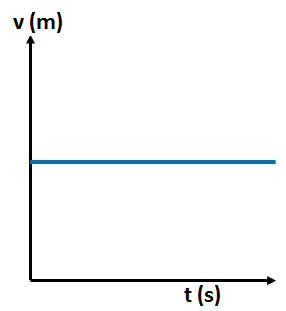
- Which controls in the car can produce acceleration or deceleration in it?
The controls in a car that can produce acceleration or deceleration are the accelerator, brakes, and steering wheel. The accelerator increases the car’s speed, the brakes slow it down, and the steering wheel changes the car’s direction, which can also result in acceleration or deceleration depending on the turn.
- If two stones of 10 kg and 1 kg are dropped from a 1 km high tower. Which will hit the ground with greater velocity? Which will hit the ground first? (Neglect the air resistance)
Both stones, regardless of their mass, will hit the ground with the same velocity and at the same time if we neglect air resistance. This is because all objects experience the same gravitational acceleration, which is approximately 9.8 m/s², in the absence of air resistance.
- A 100 g ball is just released (from rest) and another is thrown downward with velocity of 10 m/s, which will have greater acceleration? (Neglect the air resistance)
Both balls will experience the same acceleration, which is due to gravity and is approximately 9.8 m/s². The initial velocity of the second ball (10 m/s) does not affect its acceleration, as gravitational acceleration remains constant for both balls.
QIII. Give a detailed response to questions below.
- Differentiate between rest and motion. With the help of example, show that rest and motion are relative to the observer?
| Rest | Motion |
| Object does not change position with respect to a reference point. | Object changes position with respect to a reference point. |
| Object appears stationary relative to the observer. | Object appears moving relative to the observer. |
| May be at rest to one observer and in motion to another. | Always depends on the observer’s frame of reference. |
Example: If passengers are sitting on a moving train, they may consider themselves at rest because their position relative to the train does not change. However, to an observer standing on a platform, the person is in motion as they are moving along with the train. Hence, rest and motion are relative to the observer’s position.
- What are different types of motion? Define each type of motion with examples from daily life.
There are three main types of motion:
Translatory Motion:
This motion occurs when all parts of an object move in the same direction without changing its orientation.
Translatory motion is further divided into three types.
Rectilinear Motion: Movement in a straight line.
Example:
- A car moving on a straight road.
- A stone falling vertically from a height.
Curvilinear Motion: Movement along a curved path.
Example:
- A car turning around a corner.
- A football kicked in an arc.
Random Motion: Motion without a definite path or direction.
Example:
- A butterfly flying in the air.
- A kite swaying in the wind.
Rotatory Motion:
This type of motion occurs when an object rotates around a fixed axis.
Example:
- The rotation of Earth around its axis.
- The spinning of a merry-go-round.
Vibratory Motion:
This is a repeated back-and-forth movement around a mean position.
Example:
- The strings of a guitar vibrating.
- The motion of a pendulum in a clock.
- What are scalars and vectors? Give examples. How are vectors represented symbolically and graphically?
Scalars:
Scalars are physical quantities that are fully described by their numerical magnitude (size) and appropriate units.
Examples:
- Distance: The total length of the path traveled, e.g., 4.5 km.
- Speed: The rate of change of distance over time, e.g., 60 km/h.
- Time: The duration of an event, e.g., 30 seconds.
Vectors:
Vectors are physical quantities that require both numerical magnitude and direction for a complete description.
Examples:
- Force: A push or pull acting on an object, e.g., 5 N downward.
- Velocity: The rate of change of displacement, e.g., 50 m/s east.
- Acceleration: The rate of change of velocity, e.g., 9.8 m/s² downward.
Symbolic representation:
To differentiate a vector from a scalar quantity, we generally use bold letters to represent vector quantities, such as F, a, d or a bar or arrow over their symbols such as , , , or
Graphical Representation:
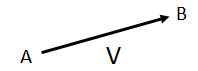
Graphically, a vector can be represented by a line segment with an arrow head. As in figure, the line AB with arrow head at B represents a vector V. The length of the line AB gives the magnitude of the vector V on a selected scale. While the direction of the line from A to B gives the direction of the vector V.
- Define the term position. Differentiate between distance and displacement.
Position:
Position refers to the specific location of an object in space relative to a reference point. It is typically described using coordinates or a reference frame, indicating where an object is situated at a given time.
| Distance | Displacement |
| The total length of the path traveled between two points. | The shortest straight line from the initial to the final position. |
| It is a scalar quantity. | Has a specific direction; it is a vector quantity. |
| Always positive or zero. | Can be positive, negative, or zero, depending on the direction of movement. |
- Differentiate between speed and velocity. Also define average speed, uniform and variable speeds, average velocity, uniform and variable velocities.
| Speed | Velocity |
| Measure of the distance covered with passage of time. | Measure of the displacement covered with passage of time. |
| It is a scalar quantity. | It is a vector quantity. |
| It is represented by v. | It is represented by . |
| Mathematically: | Mathematically: |
Average Speed:
Average speed is the total distance covered divided by the total time taken for that distance.
vave = =
Example: If a car travels 120 km in 2 hours, its average speed is 60 km/h.
Uniform Speed:
An object is said to be moving at uniform speed if it covers equal distances in equal intervals of time. This means there is no change in speed over time.
Example: A train traveling at a constant speed of 80 km/h on a straight track.
Variable Speed:
Variable speed occurs when an object covers unequal distances in equal intervals of time, meaning its speed changes over the duration of travel.
Example: A car that accelerates and decelerates in traffic.
Average Velocity:
Average velocity is the total displacement covered divided by the total time taken. It considers the direction of movement.
ave = =
Example: If a runner finishes a 400 m track in 50 seconds, their average velocity is 8 m/s in the direction of their displacement.
Uniform Velocity:
An object is said to be moving with uniform velocity if it covers equal displacements in equal intervals of time, maintaining both speed and direction.
Example: A satellite in a circular orbit at a constant speed.
Variable Velocity:
Variable velocity occurs when an object’s speed or direction changes, resulting in different displacements over equal intervals of time.
Example: A car turning around a corner at a constant speed but changing direction.
- What are freely falling bodies? What is gravitational acceleration? Write down sign conventions for gravitational acceleration? Write three equations of motion of a freely falling body?
Freely Falling Bodies:
Freely falling bodies are objects that are falling under the sole influence of gravity, with no other forces (like air resistance) acting on them. These objects experience gravitational acceleration as they fall.
Gravitational Acceleration:
Gravitational acceleration, denoted by “g” is the acceleration experienced by a freely falling object due to the force of gravity. Near the Earth’s surface, the value of gravitational acceleration is approximately 9.8 m/s². This value is constant for all objects regardless of their mass, when air resistance is negligible.
Sign Conventions for Gravitational Acceleration:
Positive (+g): When an object is falling downward in the direction of gravity.
Negative (-g): When an object is moving upward against the direction of gravity.
Equations of Motion for a Freely Falling Body:
- Draw distance-time graphs for rest, uniform speed, increasing speed and decreasing speed.
Body at Rest:
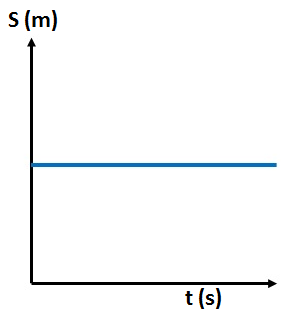
In this graph, the distance does not change over time, indicating that the object is stationary. The graph appears as a horizontal line.
Uniform Speed:
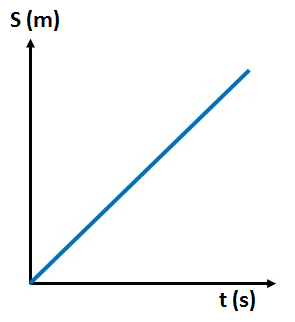
This graph shows a straight diagonal line, indicating that the distance increases linearly with time. The constant slope represents uniform speed.
Body Moving with Increasing Speed:
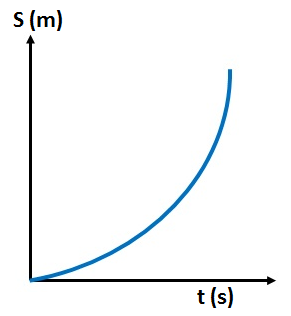
In this graph, the distance increases non-linearly with time, curving upwards. This indicates that the object is accelerating, as the distance covered in each time interval is increasing.
Body Moving with Decreasing Speed:
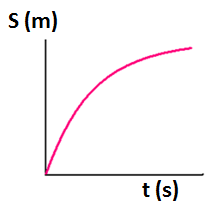
This graph shows a non-linear change in distance with time, curving downwards. The decreasing slope indicates that the object is slowing down.
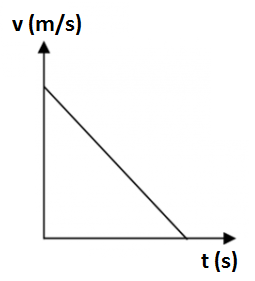
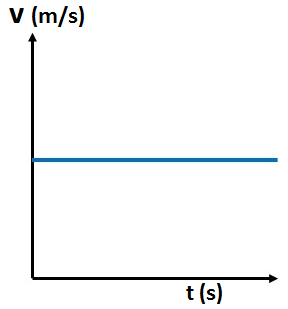
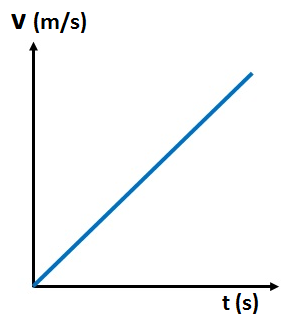
- Draw speed-time graphs for zero acceleration, uniform acceleration, and uniform deceleration. Also explain how the area under the speed-time graph represents the distance covered by the body.
For zero acceleration, the speed of the body remains constant over time, which means the graph will be a horizontal line parallel to the time axis. Since there is no change in speed, the slope of the graph is zero.
For uniform acceleration, the speed increases at a constant rate. In this case, the speed-time graph is a straight line with a positive slope. The steeper the slope, the greater the acceleration.
For uniform deceleration, the speed decreases at a constant rate. The speed-time graph in this case is a straight line with a negative slope, indicating that the body is slowing down over time.